Poznámka: Pozor pro luštitele a hádankáře, článek obsahuje řešení! Je to proti duchu výuky Richarda Pavlicka, ostatně to bylo vidět i na koncovkách na serveru http://www.bridgecz.cz/ (rok 2012), kde zveřejnění řešení koncovek nedoporučil, jako luštitel tělem i duší. Ovšem následující problém nebyl prohlášen za karetní kvíz, je to spíš záležitost informatiky.
Jak jsem vykopal poklad a ověřil jeho pravost
Tento delší a spíše technický příspěvek popisuje nemilosrdné boje a sebetrápení kolem nalezení bridžového Svatého grálu, miliónů vyřešených rozdání „dabl damy“ (DD; užívám DTH pro dvojitého tichého hráče, double dummy totiž v češtině z neformální angličtiny může znamenat dvojitý blbec). S bridžistou panem Tiborem Menyhértem jsme řešili sazbu jednoho rozdání, vlastně i méně, jen listu, jen jedné barvy, jen jedné karty, jenže já začal přemýšlet nad sazbou více rozdání, mnoha rozdání, a napadlo mě, jestli není někde nějaká existující kolekce,..., a pak se to celé zvrtlo.
Je zde samozřejmě filozofická a karetní otázka, jestli to za to hledání řešení {dabl damy} / {double dummy} / {dvojitého tichého hráče} / {hry se všemi kartami na stole} / {sehrávka s otevřenými listy} stojí, někteří hráči řešení s otevřenými listy příliš v lásce nemají, protože počet zdvihů vyjadřuje nejlepší hru obrany i hlavního hráče (nalezení např. vypadnutí honérů v singlu, zahrání těch a právě těch správných impasů, a naopak, vzdání se právě toho správného počtu zdvihů ve prospěch budoucího skvízu atd.), jak tato perfektní hra není jednostranná vůči jen jedné lince, tak je to poměrně poctivý náhled na rozdání.
Za sebe stojím samozřejmě na straně těch, kteří se analýzou zabývají, v libovolné části hry a tréninku, a dávají tomu svou váhu. Je však pravda, že bridž se s otevřenými listy nehraje a častokrát se dostaneme do suboptimálního řešení, lidé chyby dělají. Ovšem hráči si tolikrát kladou otázku co měli a mohli licitovat, jak měli sehrávat, jak bránit, že je potřeba na to mít nástroje.
Koho by zajímalo srovnání DD/DTH a skutečných sehrávek, zde je nový článkový přírůstek (květen 2013) u Richarda Pavlicka [odkaz]. Není tomu zas tak dávno, kdy server OKBridge zveřejnil výsledky svých 30 miliónů odehraných rozdání [odkaz nebo odkaz] a kolekce při BBO [odkaz] také masivně roste, jak tam průměrně hrává několik tisíc lidí 24 hodin denně.
Proč je tedy DD/DTH analýza rozdání tak cenná? Protože počítač musí prohledat stromovou strukturu celé sehrávky, to může zabrat vteřiny, minuty i hodinu výpočetního času na jedno rozdání. Laicky řečeno počítač musí sehrát všechny možnosti; ve skutečnosti jsou samozřejmě finty, jak se duplicitním možnostem vyhnout, namátkou volba karty z uzavřené sekvence 654 (je jedno, která karta bude zahrána, proto strom pokračuje jednou větví, nikoliv třemi), v tomto ořezávání je GIB od Ginsberga geniální, přínosný a jeho metody řezání rozhodovacího stromu (angl. decision tree pruning) jsou do značné míry stále výrobním tajemstvím (některé metody však publikoval ve svých článcích, namátkou zde), rychlost je však neuvěřitelná. Vlastně můžeme poděkovat Zia Mahmoodovi, že vyzval tehdejší programátory, že počítač nemůže lidské hráče porazit [odkaz]. Podobný krásný příběh je v šachách, Deep Blue versus Garry Kasparov [odkaz].
Zpět z historie k DD analýzám. Richard Pavlicek si na to vyhradil jeden počítač a deset výpočetních let. V dnešní době by se to řešilo distribuovaně (známější asi bude projekt SETI), tedy výpočty by se pustily na více počítačů, případně i za pomoci celého světa, například přes spořič obrazovky. Pak by se na centrálním počítači výsledky dávaly k sobě do jednoho souboru. I tak, 10+ miliónů stále vede soutěžní příčku, víc o tom za chvíli.
Bridžové piráty mohl totiž do nedávné doby uchlácholit vždy jen stotisícový paběrek (bez drobných) nalezený zde [odkaz], a pak originální formát knihovny ViewDDLib [odkaz; Viewer for Ginsberg's Double-Dummy Library Ver 3.3] s možností stažení legendárních 717.102 zanalyzovaných rozdání (sedm set tisíc a drobné) [odkaz] Mathewa Ginsberga, autora programu GIB (
JT852.93.KQ7.J82 AQ97.JT654.T6.A5 43.AK8.A542.7643 K6.Q72.J983.KQT9:
88887777A9A977778888
Přepis do čitelné podoby znamená liché cifry za dvojtečkou odečíst od třinácti, dostáváme:
JT852.93.KQ7.J82 AQ97.JT654.T6.A5 43.AK8.A542.7643 K6.Q72.J983.KQT9:
V Ginsbergově prohlížeči bychom to pak četli jako čtvrtou, první, třetí a druhou cifru vždy v řádku, což je blok o čtyřech cifrách v hexa (0d=0h, nula v desítkové soustavě se rovná nule v šestnástkové/hexadecimální soustavě, ..., 9=9, 10=A, 11=B, 12=C a 13=D). Pro novější formát programu Deal (aktuální verze 3.1.9) by došlo k dalšímu přeházení, o tom později. Přikládám toto rozdání jako snímek obrazovky, je to naše mapa k pokladu! Tato rozdání sloužila k potvrzení a zároveň upřesnění pravosti LOTTu [wiki, první díl, druhý díl]. Jen stručně zmíním, že LOTT pomáhá v konkurenční licitaci a místo náhodného rozhodování 50 na 50 procent (licitovat nebo nelicitovat), LOTT toto rozhodování vylepší na přibližně 70 na 30 procent. Od té doby se simulace (algoritmus Monte Carlo) a následné analýzy používají téměř pravidelně.
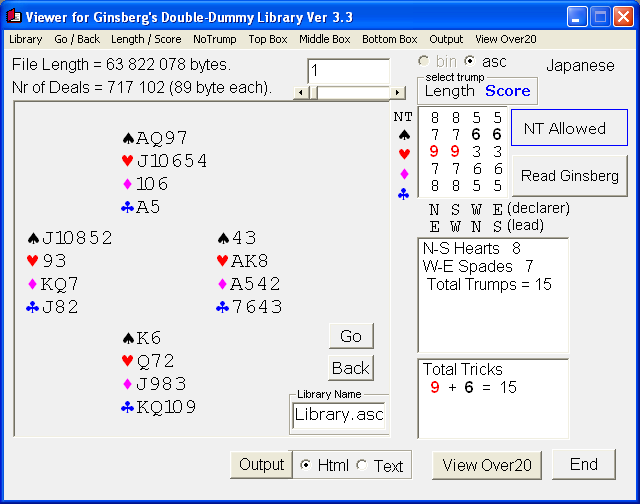
Mapa k pokladu krále Richarda!
Tolik k rozcvičce. S tímto jsem se trochu potrápil, především s tím dopočtem do třinácti v šestnáctkové soustavě, posunem karet o jednu herní pozici (standardem je začínat Severem) a také přeházením zdvihů, aby to bylo v blocích hráčů, nikoliv v blocích podle barev, ale vzbudilo to mou zvědavost po dalších dobrodružstvích! Stával se ze mě legendární zlatokop na Aljašce, který chce stále víc a nalézt nenalezené.
Pro všechny dobrodruhy mohu zmínit, že pod tím víc se skrývá legendární poklad krále Richarda s 10+ milióny rozdáními (a něco drobnými) s úplnou tabulkou dvojitého tichého hráče (angl. full double dummy table/analysis, z nekaretní oblasti to inklinuje k termínům single-dummy -> single-blind a double-dummy -> double-blind). První zmínky o něm byly podány začátkem roku 2013 na serveru Richarda Pavlicka [odkaz], králi vzdálenému příbuznému. To je ten významný zlatokop, který objevil skvíz, na který můžeme získat tři zdvihy navíc [odkaz]. Nechť mu královna, vlastně prezident Barack Obama, dopřeje dlouhého žití!
Click on Random Solved Deals for explanation.
-Richard
První indicie nás u Pavlicka zavede až na tuto webovou stránku [odkaz]. Jedná se o hackerskou věc, odkazy nikde přímo zmíněné nejsou, to mě překvapilo, jak to? Ale z internetových pravidel slušného chování jsem nikde po serveru nebrouzdal a nápad na jejich vyvěšení jsem napsal Pavlickovi mejlíkem, ten odpověděl, že tam jsou..., hmm, hackerská výzva!), přesněji v textovém souboru [rpxx.txt] je zmínka na existující databázi a její vzorek [rpxx.zip]. To jsou náhodná rozdání, podobně to pak je i pro symetrická rozdání [rpsx.txt a rpsx.zip], ta však mají jinou strukturu uložených dat. Nu, je to jako nalézt minci na pustém ostrově a víte, že jste tam správně! Je to pro vás návod, postup, vše na čem záleží!
Richard Pavlicek je však znám jako velký hádankář, takže si někde něco stáhnout a je hotovo se nedalo čekat. Je to jako legendární poklad Inků či tajemství některých faraonů, víte, že tam někde jsou, ale to je to jediné co tušíte.
Soubory Richarda Pavlicka rpxx.txt [
rpxx.zip -> rpxx.zrd [
Nu, téměř! Tohle jsem viděl! Prvních 23 bajtů, což mělo být jakože první rozdání ze čtyř tisíc, vzorek z celého toho miliónového pokladu.
Takto to vypadalo při prvním náhledu celé.

To jsem si říkal, že na celý poklad prdím, že jdu domů, ať si to řeší někdo jiný, ale přecejenom mi to nedalo. Binární soubor se skládá z nul a jedniček, takže by stačilo ty znaky dostat do šestnáctkové soustavy (viz ASCII tabulka) a pak do dvojkové. Dostáváme:
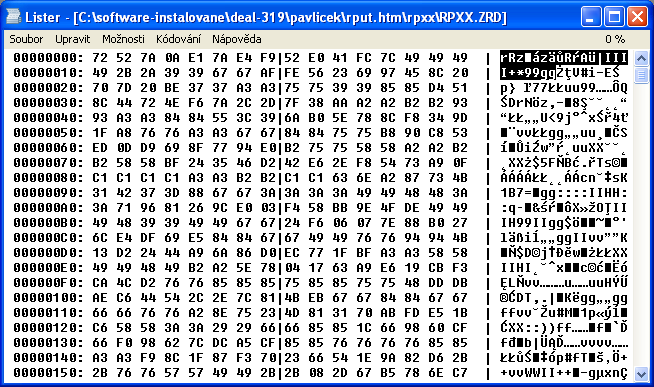
Z těch dvou šestnáctkových čísel se skládá bajt, osm bitů, resp. první a poslední čtyři bity. Teď se však muselo už sednout k programování, aby se s tím dalo pohnout. Musíme si však dát pozor jak se bity čtou, jestli normálně (v informatice či matematice u čísel zprava doleva), nebo inverzně (zleva doprava, jak čteme, tedy normálně). Co tedy je nebo není normální se stávalo relativním pojmem. To je ona jemná poznámka v rpxx.txt o Little endianu [odkaz] a obráceném řazení. Došlo tedy na to, jestli bity číst tak či onak. Navíc v návodu je, že skupina bitů (dva pro kartu a čtyři pro zdvihy) se čte samostatně, proto je návod psán v řádcích pod sebou. Než mi však tohle došlo!
Reprezentace toho samého rozdání ve dvojkové soustavě:
01010100101110000001000001111111000111110001001001010010010100
100101001001001010110010101000111001001110010110011101100111
Červenou barvou pirátovy krve jsem znázornil reprezentaci prvního bajtu (písmono
Dobrodruhům srdcem vlastním nebudu popisovat co vše jsem s těmi nulami a jedničkami zkusil/zažil. Na konci druhého dne jsem téměř vyčerpán žádal Pavlicka o radu, pokud to tedy není hádanka, a může-li mi pomoci. Poslal tip, že kódování Little endian je opravdu vztaženo na bajty, nikoliv na čtyři bity, což byl můj poslední vzorek té minuty. Áha!
Your sample.txt:
2725a7a01ea74e9f250e14cfc794949494b2a293937676
My hex dump of rpxx.bin:
72527A0AE17AE4F952E041FC7C494949492B2A39396767
So it's apparent you have swapped the high and low nibbles of each byte.
First byte is 72h = 01110010b. Second byte is 52h = 01010010b, etc.
Perhaps you thought "little endian" pertains to nibbles; but no, it only
applies to byte order.
-Richard
Ale nic! Po mnoha pokusech jsem přestával rozeznávat stranu levou a pravou stranu, vysoká či nízká mi bylo jedno, už jsem nevěděl, jestli
Jenže ráno jsem vstal a čekal mě na kompíku email, že Pavlicek rozšířil svůj BFC konvertor [Bridge File Converter, na začátku článku ve verzi 4.0, na konci sepisování ve verzi 4.3, bfc.txt a bfcsetup.exe] o tyto dva formáty (z dosavadních 10, včetně PBN, LIN a dalších, speciálně výhodná je LIN->PBN konverze v těchto dnech), o ZRD (Richard's Solved Random Deals) a ZSD (Richard's Solved Symmetric Deals), a že by mě to možná mohlo i zajímat! Možná taky zajímalo a jak! Vstal jsem z (polo)mrtvých.
Aha, říkal jsem si, takže nakonec to přecejenom běžné binární soubory byly i nebyly! Takový podvod i nepodvod na ubohého řešitele. Karetní bůh se smiloval nad smrtelným nešťastníkem! Do kronik vepište a na hrob mi dejte: Léta Páně 2013, 17. května, BFC, verze 4.3.
This may interest you... The file RPXX.BIN is now named RPXX.ZRD to identify the file format, which my Bridge File Converter will now convert automatically to any other format. (Likewise, files RP01.BIN to RP10.BIN are now RP01.ZRD to RP10.ZRD.)
Similarly, the solved symmetric deals (RPSX.BIN and RPSD.BIN) are now RPSX.ZSD and RPSD.ZSD to identify another format that my BFC now converts.
-Richard
Nalilo to do mě novou krev, když už jsem to vzdal, tak to zkusím dorazit jen tak, už jen pro zábavu. Než dorazila vidina řešení, tak jsem mohl (dokonce automatem, kdyby na to přišlo) kontrolovat, zda-li každý hráč má 13 karet (když se sešlo moc nul, měl moc karet Západ, když moc jedniček u sebe, měl jich mnoho Jih ap.), dále, zda-li počet zdvihů je v rozmezí 0 až 13 karet (lítalo to do 15, když se sešly čtyři jedničky). Takový postup jsem vyřadil hned, občas tyto ukazatele seděly a pak neseděly počty zdvihů vůči nezávislému propočtu. Tedy rozdání bylo zdánlivě karetně v pořádku, počty zdvihů zdánlivě také, ale neseděly k sobě.
Abych věděl, kde je první a kde poslední rozdání z oněch 4000, tak jsem si na úrovni bajtů (Ctrl+C a Ctrl+V by nám nestačilo, neb jsou tam řídicí znaky, to jsou znaky v šestnáctkové soutavě 00 až 1F; je to vidět i na naší ukázce na čtvrtém znaku, kdy HTML zakazuje řídicí znaky zobrazovat a je tam mezera), který v hexa či binárně, vyextrahoval prvních 23 bajtů do souboru exp.zrd [
bfc.exe exp.zrd p
Získal jsem veledůležitý rozpis prvního rozdání v souboru out.pbn [
% PBN created by BFC.EXE exp.zrd p
[Event ""]
[Site ""]
[Date ""]
[Board ""]
[West ""]
[North ""]
[East ""]
[South ""]
[Dealer ""]
[Vulnerable ""]
[Deal "W:K9.KQT3.743.QJ95 J873.J42.Q65.KT2
AT652.A976.AJ82. Q4.85.KT9.A87643"]
[Scoring ""]
[Declarer ""]
[Contract ""]
[Result ""]
{RBNM ::44236=:99B97+99A97}
A zobrazil jsem si to něco už jako bridžové rozdání. DD/DTH analýza je ta tabulka uprostřed, kde je obvykle bridžový stůl.
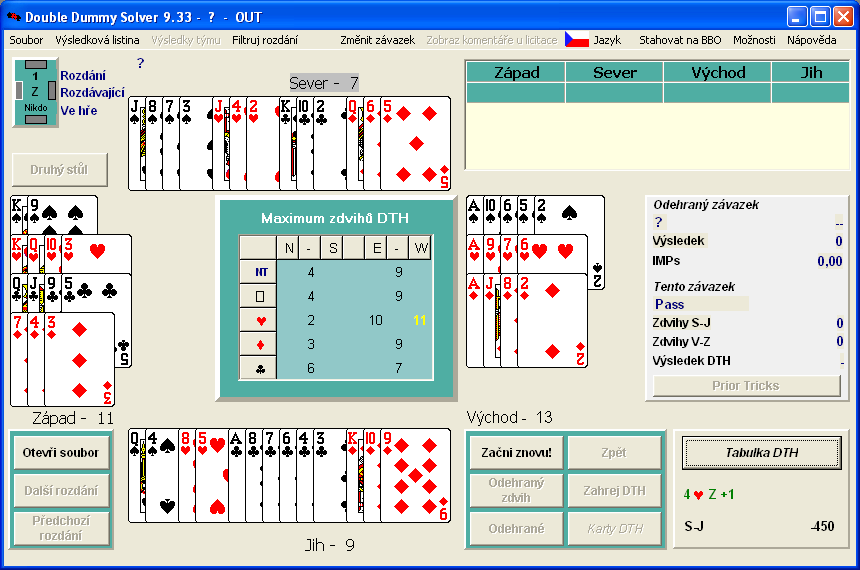
(V roce 2011 jsem se pokusil přeložit rozhraní u programu DD Solver [odkaz], připomínky prosím posílejte emailem, kdyby něco bylo chybně, zkusil bych to zapracovat a autorovi bych zaslal opravenku.)
To jsem si říkal, že to nevzdám a šel jsem za tím jak uslintaný bernardýn! Začal jsem od řešení jít zpátky kam to jen šlo, eso pikové je u Východu, Východ je v návodu (00 Západ, 01 Sever, 10 Východ, 11 Jih) jako binární hodnota 10, další karta je král pikový u Západu atd. Dostal jsem řadu:
10 00 11 01 | 10 00 01 01 | ...
A K Q J |
T 9 8 7 | ...
Slzy radosti jsem měl na krajíčku očí, tímto musí řada začít nebo končit a srovnal jsem to se svými pokusy. Bohužel nikde nic. Pokračoval jsem rozkladem ve dvou bitech u karet a ve čtyřech bitech u zdvihů. A pak jsem to uviděl! Úplně někde v dáli.
Když prohodím bajty (dva hexy) od konce (reverzně alias Little endian), tedy končím sekvencí, kterou jsem začínal: ...e1 0a 7a 52 , dám do binární řady, budu číst uvnitř bajtu vždy dva bity zprava doleva (lidsky reverzně), ale se zápisem zleva doprava (informaticky reverzně), dostáváme (začínáme to číst nulou na druhém řádku):
... | 01010010 | 01110010 ||
... | efcdab89 | 67452301 ||
Vyzískáme, čteno od konce, řadu začínající
494949492b2a39396767Dekódované:
94 949494b2a293937676To je v pořadí Západ, Sever, Východ, Jih, a to už můžeme vyčíst z náhledu v programu Double Dummy Solver (DDS).
Šťastný jsem byl jako blecha!
Můj drobný program v Pythonu dvojkové řady [odkaz; aktuálně ve verzi 2.7.3] konečně vypsal tížené, tedy:
Rozdání 1
[['K', '9'],['K', 'Q', 'T', '3'],['7', '4', '3'],['Q', 'J', '9', '5']]
[['J', '8', '7', '3'],['J', '4', '2'],['Q', '6', '5'],['K', 'T', '2']]
[['A', 'T', '6', '5', '2'],['A', '9', '7', '6'],['A', 'J', '8', '2'],[]]
[['Q', '4'],['8', '5'],['K', 'T', '9'],['A', '8', '7', '6', '4', '3']]
[[9, 4, 9, 4],[9, 4, 9, 4],[11, 2, 10, 2],[9, 3, 9, 3],[7, 6, 7, 6]]
První řádek jsou karty Západu, druhý pak Severu, třetí Východu a předposlední řádek patří Jihu, vnitřní entici tvoří karty, seřazené zleva: piky, srdce, kára a trefy. Karty v barvě jsou setříděné sestupně. Pátý řádek jsou právě zdvihy, vnější entice je zleva bez trumfu až po trefy a vnitřní entice od Západu po Jih. Tohle pak už konvertítko přeházelo, jak bylo potřeba.
Program byl za zásluhy a věrné služby povýšen do šlechtického stavu! To však ještě konvertítko nevědělo, čeká jej ještě mnohé překvapení: milióny rozdání, tohle byl jeden kus. Jinak těch deset miliónů rozdání žádný bridžový hráč nezvládne sehrát. Kdyby člověk zvládl 300 rozdání denně (Je to reálné? Možné to asi je u bridžových marathonů po kratší období.) a hrál 300 dní v roce po dobu 50 let, tak se dostane na cca slabší polovinu (4.500.000 rozdání). Snad jsem se neustřelil v nějaké té nule.
Důvěřuj, ale prověřuj!
Ale co nezávislá kontrola? Ne že bych Pavlickovi, jako Grandmasterovi/Mistrovi, nevěřil, ale pirát je pořád pirátem a pirátem zůstane. Nevěřím mu! Vědecká presumpce viny! Vědec je vinen za své pokusy, dokud vědecky neprokáže opak.
Mohl jsem to zkontrolovat rovnou v DDS, ale co když tyto Pavlickovy výsledky program z PBN přebírá, to není žádná kontrola! Musel bych editovat PBN soubor a zkusit DDS znovu. Nebo byla potřeba pomocného programu, který odevzdá v rozumném formátu jen karty a zdvihy se dopočítají. Takový automatizační nástroj máme.
Provedu vás v pěti minutách bridžovou hračkou, programem Deal [odkaz], takový vstup pro neznalé. Těchto hraček v průběhu dvaceti let najdeme mnoho [odkaz či odkaz], ale Deal se uplatnil, neb je volně dostupný, se zdrojovými kódy, je programovatelný a i firma BBO jej snadno implementovala. Člověk by si řekl, že je jedno, jak se těch 52 karet rozdá, nu, není to jedno! Existuje dokonce celá oblast pravděpodobnosti a matematické statistiky, která měří vyčíslitelnou náhodnost těchto pseudonáhodných čísel (angl. randomness). Fyzici tvrdí, že mají už skutečný náhodný generátor, ale matičce Přírodě bych kolem náhody zrovna nevěřil [odkaz]. Měří se buď atmosférický šum, nebo kosmický šum, nebo se měří fotoluminiscence ap., a to se převádí z videa (zvuk a/či obraz) na bity. Takže už žádné házení hrací kostkou, volbu cifer od čísla pí či nedejbůh matematicky exaktně jako u dnešních pseudonáhodných čísel, dodávám s úsměvem.
Dodatek: BBO téměř jistě generuje rozdání vlastními prostředky, na testování a pro generování pro uživatele používá program Dealer [odkaz]. To je alternativa programu Deal z dílny Hans van Staverena [odkaz]. Navíc autor v manuálu dokonce nedoporučil svůj program na rozdání pro turnaje, neb si není jistý dostatečnou náhodností. Zajímavou variantou (vygenerování 10000 rozdání a vybrání těch „ulítlejších“) mají zde [Hand Generator – Goulash]. To se hodí na speciální tréninky a do společenského prostředí.
Zpět do informatické reality. Program si stáhneme do své složky z těchto stránek [odkaz], rozpakujeme. Uvážím verzi pro Windows, Linuxáci znají. Najdeme tam především spustitelný soubor deal.exe. Z příkazové řádky si můžeme zkusit po zapsání a potvrzením klávesou Enter tento první experiment:
deal 1
Obdržíme pseudonáhodně vygenerované rozdání:
S: AKJ4 H: J96 D: 98 C: KJT5 S: Q832 S: T965 H: AK8732 H: QT D: 2 D: 765 C: 64 C: Q987 S: 7 H: 54 D: AKQJT43 C: A32 ----------------------------
Zde přikládám další tipy:
deal 20
deal -l 20
deal -i format/ddline 20
V prvním případě se vypíše dvacet rozdání v článkovém formátu, v druhé ukázce rozdání vměstnané do jednoho řádku a v poslední ukázce dvacet rozdání, ale s dopočtem maxima zdvihů pro obě linky a všechny barvy i beztrumfový závazek.
Programátoři zajásají, že se s tím dá dát dál hrát, nastavit podmínky a omezení všeho možného i nemožného atd., přeskakuji, to je na samostatný příspěvek (zvlášť důležité je, že můžeme konkrétnímu hráči zafixovat karty, například jednomu všech 13 nebo dvěma hráčům 26 karet a rozdávat zbylé karty, to je klíčové pro všechny analýzy: ať už u licitace, výnosu, obrany i sehrávky) či překlad manuálu autora programu, zde se zaměříme na výpis do souboru, to bude takto:
deal -l 1 >rozdani.txt
V souboru rozdani.txt
[
K7543 K5 AT KT84|AQJ98 J87 653 Q5|2 AT962 J8742 J7|T6 Q43 KQ9 A9632
Do souboru rozdani.txt se nám uloží jedno rozdání bez DD zdvihů. To však můžeme znovu vzít a nechat DD dopočítat plus výstupy rovnou přesměrujeme do souboru rozdani-reseni.txt [
deal -I "line rozdani.txt" -i format/ddline >rozdani-reseni.txt
Dostáváme v tomto souboru:
K7543.K5.AT.KT84|AQJ98.J87.653.Q5|2.AT962.J8742.J7|T6.Q43.KQ9.A9632
|6 9 9 6 5|7 4 4 6 7|6 8 8 5 5|7 5 5 7 8
Pozn. Pokud bychom místo jedničky dali například 32, tak za pár desítek minut budeme mít v souboru rozdani-dd.txt [
-l), nebo i s DD:
deal -i format/ddline 32 >rozdani-dd.txt
To je přesně to, co kvůli kontrole potřebujeme. Na vstupu budeme mít 52 karet, na výstupu výpočty zdvihů. Jen předesílám, že si musíme dát pozor na to, kolik rozdání v souboru máme, standardně Deal pracuje jen s desítkou souborů, není-li zadána hodnota, musíme mu to upřesnit číslem, přesněji vstupním parametrem programu.
Jedna poznámečka. Podrobnou nápovědu, návody a ukázky najdeme na oficiální stránce autora [odkaz], kratičkou nápovědu dostaneme zapsáním chybného parametru:
deal -h
Získáme:
deal: invalid option -- h
usage: deal [-v] [-s seed] [-i includeFile] [-I inputFormat] [count]
Vidíme následující: podrobnější výpis běhu programu (-v, verbose), nastavení počáteční hodnoty pro pseudogenerátor (-s, seed), vstupní/zpracovávaný soubor (-i, include), načítaný/výstupní formát (-I, input) a počet rozdání (count, číslo). Především nás zajímá přepínač -s, tím totiž dostaneme pseudonáhodné řešení (jinak se nejčastěji volí přepis systémoho času počítače), ale tento parametr nám zajistí, že to samé rozdání dostaneme znovu. Takto bychom byli například schopni reprodukovat dřívější sadu rozdání (jinak nemáme šanci se k rozdání znovu dopracovat, systémový čas pracuje s milisekundami; jen obecně pozor, že algoritmy generování se se změnou verze programu mohou změnit, mám to neblaze ověřené u Pythonu, i když dokumentace to zmínila):
deal -s 10000 -l 1
Při opětovném spuštění této řádky vy i já dostaneme naprosto to samé, tedy:
A975 AT74 K5 543|Q2 K8532 T4 AQ76|JT86 Q96 J963 JT|K43 J AQ872 K982
Musíme si dát pozor na několik věcí, pokud používáme tento druh reprodukovatelného pseudonáhodného generování, nesmíme použít tu samou hodnotu několikrát, pak by turnaj byl se stejnými rozdáními. Hodnota může být záporné číslo (což systémový čas nikdy nebude), ale je to celočíselná hodnota a musíme si dát pozor, v jakém intervalu se smíme pohybovat.
Když zapíšeme (je tam tucet devítek):
deal -s 9999999999990 -l 1
A opětovně spustíme, dostaneme to samé rozdání, vše je zdánlivě v pořádku. Jenže když zapíšeme hodnoty blízké, např. 9999999999989 či 9999999999991, dostaneme opět to samé rozdání.
deal -s 99999999989 -l 1
deal -s 99999999990 -l 1
deal -s 99999999991 -l 1
nebo hlouběji:
deal -s 999999999999 -l 1
deal -s 9999999999999 -l 1
deal -s 99999999999999 -l 1
Nepomůžeme si ani velkými zápornými čísly. V následujícím bloku sice obdržíme jiné rozdání než doposud, ale princip je stejný a získáme stejné rozdání pro tuto šestici:
deal -s -99999999989 -l 1
deal -s -99999999990 -l 1
deal -s -99999999991 -l 1
nebo hlouběji:
deal -s -999999999999 -l 1
deal -s -9999999999999 -l 1
deal -s -99999999999999 -l 1
Ani práce s desetinnými čísly nepomůže. Desetinná část je odstraněna, uříznuta, nikoliv zaokrouhlena.
deal -s 1.4 -l 1
deal -s 1.5 -l 1
deal -s 1.6 -l 1
to samé i s desetinnou čárkou:
deal -s 1,4 -l 1
deal -s 1,5 -l 1
deal -s 1,6 -l 1
Děsivé, že? A hlavně nepřijatelné. Důvod je ten, že Deal příliš velké, kladné či záporné hodnoty, nastaví na nejbližší přípustnou kladnou/zápornou hodnotu a s tou pracuje. Takže pokud byste v pondělí použili obrovské číslo končící 89, v úterý 90 a ve středu 91, všichni přítomní by se divili.
Formálně z pohledu programování je to v pořádku, ale když dojde k takovému vnitřnímu zásahu (vypadá to na zlom někde kolem deváté-desáté cifry), uživatel by měl být informován výpisem zprávičky od programu. Ještě lépe by měl být uživatel požádán o zadání čísla v určitém rozsahu. Přesně to nemám ze zdrojových kódů zjištěné, ale ten použitelný radius se pohybuje kolem plus mínus devíti cifer. Zároveň to píši autorovi programu, že se program chová zvláštně/nebridžově v této situaci a není to hlídáno. Ten, kdo použije své rodné číslo plus například číslo roku, měsíce a dne v roce (9 nebo 10 cifer), by měl už problémy.
Mj. na rok+měsíc+den velký pozor, jejich součet bez řídicích nul není vždy rozdílný, například:
20. května 2013 (20+5+2013=2038),
je to to samé jako například:
19. května 2014 (19+5+2014=2038),
jako počáteční hodnota pro pseudogenerátory je tedy tento součet nevhodný, není jedinečný. Proto se používá časová známka (angl. timestamp), což je přepis den-měsíc-rok 20
Informatici, budou-li se tak v budoucnu nazývat, já tipuji termín virtualizátoři, budou řešit zajímavý technický problém na přelomu roku 9999 a 10000, kdy se budou muset zpětně přehodnotit čtyřciferné roky na nula+rok, tedy letošní rok, 2013, by byl zapsán jako 02013. Ale to není aktuální problém. Značka se z osmi cifer stane devíticifernou, takže jednoznačná bude, jen ta délka řetězce se změní a to může ovlivnit parsování.
Až někdo objeví, jak se tato počáteční hodnota pseudogenerátoru na BBO nastavuje, má šanci se dostat k rozdáním ještě před vlastní hrou na BBO. Kdo by to však dělal, že? Bridž by nebyla taková zábava.
Před lety i před pár týdny jsem na BBO Forums napsal, že by se hodilo, kdyby tabulka DD byla k vidění po sehrávce. Ale jen tak to není. Pokud výpočet může zabrat i hodinu, bylo by potřeba generovaná rozdání předvypočítat (zdvihy, případně i par/minimax), uložit do fronty, a to není zas tak jednoduché než když jen nabídnete prosté rozdání 52 karet, což se dá udělat na koleně do sekundy i v pomalém programovacím jazyce.
Vraťme se do pirátské reality. Teď došlo opět na Python. Svého Konvertora jsem rozšířil o výpis a pasoval na Velkého konvertora, záměrně jsem to parsoval na co nejmenší elementy (entice uvnitř entic), abych se později vyhnul zpětnému parsování, např. „S“ pro eso pikové v „SA“ ap.
Spuštění je:
python konvertor.py rpxx.zrd
Už se na pustém ostrově ztrácím při cestě od pokladu, ale Konvertor vypsal dva soubory, 1testuj.txt [
J873 J42 Q65 KT2|AT652 A976 AJ82 |Q4 85 KT9 A87643|K9 KQT3 743 QJ95
A druhý soubor, 2overen.txt [
J873.J42.Q65.KT2|AT652.A976.AJ82.|Q4.85.KT9.A87643|K9.KQT3.743.QJ95|
4 2 3 6 4|9 10 9 7 9|4 2 3 6 4|9 11 9 7 9
Vidíme, že se oddělovače mezi barvami v Dealu liší, ale to už Konvertor zvládá.
První soubor podstrčíme Dealu na výpočty a rovnou výsledky vypíšeme do pomocného souboru 3deal.txt [
deal -I "line 1testuj.txt" -i format/ddline 32 >3deal.txt
Pokud pracujete s CygWinem [odkaz] a nebo již rovnou na Linuxu či Mac OS X, tak máme k dispozici nástroj diff ke srovnávání souborů. Spustíme jej takto:
diff 2overen.txt 3deal.txt
Nástroj diff nic nenapíše, takže jsou soubory identické, na úrovni všeho, na úrovni řádků, rozdání, bajtů, bloku bitů, atomů, kvarků, ale hlavně bitů! Dobře to Pavlicek spočítal, dobře!
Poněvadž jsou soubory identické, je jedno, který použijeme na konverzi do něčeho vstřebatelného pro lidské oči:
deal -I "ddline 2overen.txt" -i format/par 32 >4deal.pbn
nebo
deal -I "ddline 3deal.txt" -i format/par 32 >4deal.pbn
Získáme v souboru 4deal.pbn [
[Date "1965.01.01"]
[Board "1"]
[West "West"]
[North "North"]
[East "East"]
[South "South"]
[Dealer "N"]
[Vulnerable "None"]
[Deal "N:J873.J42.Q65.KT2 AT652.A976.AJ82. Q4.85.KT9.A87643 K9.KQT3.743.QJ95"]
[Contract "4H"]
[Declarer "W"]
[Result "11"]
[Score "NS -450"]
{
S: J873
H: J42
D: Q65
C: KT2
S: K9 S: AT652
H: KQT3 H: A976
D: 743 D: AJ82
C: QJ95 C: ---
S: Q4
H: 85
D: KT9
C: A87643
north makes 6 tricks in clubs
north makes 3 tricks in diamonds
north makes 2 tricks in hearts
north makes 4 tricks in spades
north makes 4 tricks in notrump
east makes 7 tricks in clubs
east makes 9 tricks in diamonds
east makes 10 tricks in hearts
east makes 9 tricks in spades
east makes 9 tricks in notrump
south makes 6 tricks in clubs
south makes 3 tricks in diamonds
south makes 2 tricks in hearts
south makes 4 tricks in spades
south makes 4 tricks in notrump
west makes 7 tricks in clubs
west makes 9 tricks in diamonds
west makes 11 tricks in hearts
west makes 9 tricks in spades
west makes 9 tricks in notrump
}
[Auction "N"]
Pass Pass Pass 4H
[Play "N"]
*
Informace o zdvizích v komentáři jsou seřazeny zas úplně jinak než doposud... Člověk by si měl vzít pirátskou bambitku a odprásknout se.
Deal nás jen informuje, které rozdání zpracovává, kdo je rozdávajícím (točí se ve směru hodinových ručiček) a kdo je ve hře (točí se proti směru hodinových ručiček). Takto to vypadá pro 32 rozdání:
Computing par for deal 1 north None
Computing par for deal 2 east NS
Computing par for deal 3 south EW
Computing par for deal 4 west All
Computing par for deal 5 north NS
Computing par for deal 6 east EW
Computing par for deal 7 south All
Computing par for deal 8 west None
Computing par for deal 9 north EW
Computing par for deal 10 east All
Computing par for deal 11 south None
Computing par for deal 12 west NS
Computing par for deal 13 north All
Computing par for deal 14 east None
Computing par for deal 15 south NS
Computing par for deal 16 west EW
Computing par for deal 17 north None
Computing par for deal 18 east NS
Computing par for deal 19 south EW
Computing par for deal 20 west All
Computing par for deal 21 north NS
Computing par for deal 22 east EW
Computing par for deal 23 south All
Computing par for deal 24 west None
Computing par for deal 25 north EW
Computing par for deal 26 east All
Computing par for deal 27 south None
Computing par for deal 28 west NS
Computing par for deal 29 north All
Computing par for deal 30 east None
Computing par for deal 31 south NS
Computing par for deal 32 west EW
Formát PBN [odkaz], znám i šachistům, si můžete otevřít ve vašem oblíbeném bridžovém programu. Formát sice drobně Pavlicek kritizuje, že se dá stáhnout na třetinu původní velikosti, ale to je drobnost.
My se hlavně dozvíme, že u prvního rozdání je par/minimax 4format/par, resp. alias format/gibpar, nebo format/parArticle). Umí to i Double Dummy Solver a další produkty.
Jak si vypsat všechny závazky rovny paru (může to být závazek hrán od obou stran stolu, můžeme například mít rozdání, kde je možné hrát 2
Nebo, nebo si ještě v rychlosti můžeme vyřešit i tento problém. Například kdo bude rozdávajícím 1634. rozdání a v jaké hře budou linky?
Poněvadž se běh opakuje pro čtyři hráče, budeme se zabývat dělením po zbytku čtyřmi, proto hráče zaznačíme 0 pro Sever, 1 pro Východ, 2 pro Jih a 3 pro Západ. Zbytek po dělení čtyřmi 4 bychom nikdy nedostali (zbytek je nula). Sever tedy bude hrát 0, 4, 8, 12, ... rozdání. Číslování rozdání však začíná jedničkou, tedy od zadaného čísla pořadí odečteme jedničku. Zjistíme zbytek po dělení čtyřmi a dle klíče vypíšeme hráče.
1634 mínus 1 je 1633. Po vydělení čtyřmi získáváme 408,25, desetinná část je 0,25 a zpětně vynásobíme čtyřmi. Zbytek je 1. To je Východ. Je to spočteno na řádku 10, vypsáno na řádku 14 dále uvedeného zdrojového kódu.
Pozn. Tibor Menyhért na to šel ještě efektivněji. Zjistil zbytek po vydělení čtyřmi a přiřadil si ke hráči rovnou. Tedy Sever=1, Východ=2, Jih=3 a Západ=0.
Těžší situace je spočítat hru, když je pohyb proti směru hodinových ručiček, zkusíme si to představit přes tuto pomůcku.
| 0 | ||||
| 0 | 1 | |||
| 0 | 1 | 2 | ||
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 3 | |
| 1 | 2 | 3 | ||
| 2 | 3 | |||
| 3 |
Takto bychom si mohli představit hru pro dvacet rozdání. Hra se posouvá zvrchu dolů ve sloupci a zleva doprava. Důležitá je změna na první pozici u čtyř rozdání, je to ten pátý řádek. Prvně to byla nula (Nikdo), pak jednička (linka Sever-Jih), poté dvojka (linka Východ-Západ) a nakonec trojka (Obě linky). Takže se nám hodnota vždy přičte o jedničku po každé čtveřici, tedy k číslu rozdání přičteme celočíselnou hodnotu (uřízneme desetinnou čárku a vše od ní vpravo) po vydělení čtyřmi. Poněvadž bychom mohli dostat hodnotu vyšší než 3 (např. u čtrnáctého rozdání (mínus ona magická jednička) to je 13+3), což je 16), tak tento mezivýpočet znovu proženeme kalkulátorem a vezmeme jen zbytek po vydělení čtyřmi. To je nula a nikdo není ve hře.
Jak to však bude od 17. rozdání dále? 17. rozdání je stejné jako první atd. Takže bychom mohli zvažovat zbytek po dělení šestnácti, ale to je zbytečné. 16 je násobek čtyř.
Pojďme konkrétně k našemu 1634. rozdání? Upravíme hodnotu na řadu začínající od nuly o jedničku na 1633. Dále 1633+1633/4=2041,25 a odřízneme desetinnou část, tedy 2041. Zbytek po 2041/4 je 1. Linka Sever-Jih bude ve hře, druhá nikoliv. Výpočet je na řádku 11 a vypsání je na řádku 15 ve zdrojovém kódu.
Aby si přišli na své i sazeči, zde je drobný Python zdrojový kód (aktuální verze dvojkové řady je 2.7.4), vysázený přes Pygments [odkaz] do PNG (přímo mi to nešlo, přednastavené kódování Latin1 nebere písmena š, ž a další, a přepnout se do UTF-8 sice šlo v /pygments/formatters/img.py, ale beze změny k lepšímu), tedy přes prostředníka do HTML, přítele Pátka u Robinsona, následně převedený z HTML do PNG přes Python knihovnu wkhtmltopdf [odkaz], takové rozumné udělátko do automatizační nepohody. Zdá se mi to lepší, než klikátko typu Pearl Crescent Page Saver [odkaz]. Nakonec jsem se přiklonil ke zveřejnění HTML místo PNG kvůli velikosti na disku, zde jest uložen pod rozdava.py [
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #!/usr/bin/env python
#encoding=utf-8
t=1634 # Rozdání, které mě zajímá, zde se dá dát cyklus...
rozdavajici=["Sever","Východ","Jih","Západ"] # Konstanty rozdávající.
vehre=["Nikdo","Sever-Jih","Východ-Západ","Obě linky"] # Konstanty hra.
try: t=int(t) # Pokus o převod na číslo.
#Nebo nastala chyba, nastavuji jedničku, která se stane nultým rozdáním.
except: print "Převádím vstup na první rozdání."; t=1 # Změna při chybě.
t+=-1 # Úprava na pořadí od nuly.
rozdava=t%4 # Zbytek po dělení čtyřmi (rozdávající).
je=(t+t//4)%4 # Posun o celý násobek a zbytek po dělení čtyřmi.
print "Rozdání č. "+str(t+1) # Co mě zajímalo.
print "Pořadí od nuly:",str(t) # Vnitřní úprava.
print "Rozdává",rozdavajici[rozdava] # Kdo tedy rozdává.
print "Hra:",vehre[je] # Vypiš na obrazovku výsledek.
|
Takto byl vysázen, do designu pygments.css [
pygmentize -f html -O encoding=utf-8,linenos=1
-l python -o rozdava.htm rozdava.py
pygmentize -S colorful -f html >pygments.css
Pro rozdání číslo 1634 (zadané na třetím řádku zdrojáku) nám tento drobný prográmek vypíše následující čtyři řádky (python rozdava.py):
Rozdání č. 1634
Pořadí od nuly: 1633
Rozdává Východ
Hra: Sever-Jih
Teď se dá program obalit cyklem či číslo rozdání si vyžádat od uživatele při spuštění atd. Možností je celá řada, záleží na potřebě.
Pozn. Tibor Menyhért na to šel opět programátorsky efektivněji, i když hledání zbytku po vydělení 16 se nedá z hlavy téměř spočítat (oproti zbytku po vydělení 4, což se ještě jakž takž dá). Tedy posuny se opakují v každých 16 rozdáních. Na to si připravil pole a posuny upravil vnitřně, není potřeba žádných výpočtů či dopočtů, jen se zbytku po vydělení 16 přiřadí už konkrétní hodnota, 0=Žádná linka, 1=linka Sever-Jih, 2=linka Východ-Západ, 3=Obě linky.
$hra=array(2, 0, 1, 2, 3, 1, 2, 3, 0, 2, 3, 0, 1, 3, 0, 1);
Post Mortem: celý poklad
Nyní však již vážně. Na ZRD/ZSD soubory lze použít toto konvertítko. Získáme tím rozdání s/bez zdvihů ve formátu vhodném pro program Deal.
python konvertor.py rp01.zrd
A z tama můžeme konvertovat dále do některého formátu ve složce /format/, případně si v Dealu či úpravou Konvertora v Pythonu doprogramujeme vlastní formát.
Já jsem si ještě navíc zkontroloval počet řádků:
cat 1testuj.txt | sed -n "$="
nebo
cat 2overen.txt | sed -n "$="
Výsledek byl správný, tedy 1.048.576 rozdání v první části z celkových desíti.
Na prvním souboru mi vše sedělo. Zkusil jsem i jednoduchou optimalizaci Python kódu. Zápis velkého množství dat do souboru byl méně výhodný než malý (skoro dvojnásobně), zapnutý Indian (což mělo být zjednodušení) dávalo průměrně horší výsledek o tři čtvrtě minuty než když byl zapnutý. Načtení souboru po 23 bajtech nebo celý a pak jeho parsování nemělo vliv. Konvertor zvládl svou práci za průměrně 5 minut. Můžeme vyjádřit relativní spokojenost.
Nyní to samé přes BFC. Stáhneme si do složky s Pavlickovým konvertítkem tyto soubory (pozor, jde se po rozbalení do 450 MB, ale co to dnes je, že, taková zdravá polovina filmu CD kvality či DVDRipu):
Aktualizace 11. 6. 2013: Na přání Richarda Pavlicka byly přímé odkazy na bridžový poklad (ZIP soubory) ukryté na jeho serveru odstraněny (jeho server je přetížen i tak), detaily na ně hledejte v tomto souboru [odkaz, resp. odkaz], případně mi napište email a já vám odkazy obratem zašlu.
Soubory si rozpakujeme a podstrčíme Pavlickovu konvertítku, jenže do jakého formátu?
Pavlickův konvertor do PBN formátu to zvládl za 15 vteřin (velikost souboru 286 MB), do textového formátu za 23 vteřin (velikost souboru 532 MB). Tedy žádná miminka! Padnul by na pevném disku celý film. Zde je kompletní sumář jeho výstupních 13+1 formátů u poslední verze BFC (květen 2013):
| Pořadí | Formát | Velikost (bajty) | Čas (s) | Poznámka |
| 01 | TXT (t) | 553.753.193 | 33,7 | Plain Text |
| 02 | RBN (r) | 83.685.060 | 08,8 | Richard's Bridge Notation |
| 03 | RBX (x) | 81.587.907 | 08,9 | Richard's Inline Notation |
| 04 | LIN (l) | 126.676.653 | 09,7 | Bridgebase Online (BBO) |
| 05 | PBN (p) | 300.740.265 | 10,8 | Portable Bridge Notation |
| 06 | EML (e) | 677.773.364 | 21,2 | OKbridge Email |
| 07 | REC (c) | 415.235.397 | 12,4 | OKbridge Recording |
| 08 | DAT (d) | 218.264.359 | 11,4 | Deep Finesse |
| 09 | 117.009.245 | 10,2 | DDline (Thomas Andrews) | |
| 10 | 94.371.840 | 20,4 | Ginsberg DD Library (ASCII) | |
| 11 | 27.262.976 | 09,1 | Ginsberg DD Library (binary) | |
| 12 | DUP (u) | 163.577.856 | 16,2 | Duplimate |
| 13 | PPL (b) | 809.500.674 | 24,7 | Bridge Baron |
| 14 | 24.117.248 | 09,1 | Richard's Solved Random Deals | |
| 15 | 6.291.456 | 08,8 | Richard's Solved Symmetric Deals | |
| -- | HTM (h) | 755.049.390 | 26,1 | HTML à la Richard Pavlicek |
Srovnání výstupů pro desetinu pokladu (konverze souboru
rp01.zrd).
Jedná se o 1.048.576 rozdání (jeden milión a nějaké drobné).
Právě mi na disku padnulo místo velikosti DVD z prvního ZIP souboru, asi to zas smažu, poklad jeden, utopím se v tom bohatství. Černě jsou zaznačeny formáty před mým hledáním řešení a v původním konvertoru Pavlicka (verze 4.0),
Hi Pavel,
You must be my project manager. :) Download the latest BFC (4.3) which now includes DDline format. I couldn't find a standard file extension for it, so I chose DDL (my Type I because D and L are taken). I also revised the table in BFC Main per your suggestion.
Let me know if the DDL works for you. (I tested it with my 10 MB database, back and forth, without error.)
-Richard
Můžeme si povšimnout dalších vlastních formátů Richarda Pavlicka, RBN a RBX [odkaz]. Přikládám vzorek pro první rozdání,
out.rbn [
out.rbx [
Program Deal neměl ani navolenou příponu, tak ji Pavlicek zavedl (DDL) a o tom jsem s radostí napsal Thomasi Andrewsovi. Krásně se to plete s DLL, což je také knihovna, ale pro programátory.
Spuštění PY nebo PYC nehrálo v rychlosti roli, soubor jsem získal překompilováním (python kompiluj.py) následujícího uloženého ve zvláštním souboru kompiluj.py [
import py_compile
py_compile.compile("konvertor.py")
Co se člověk všechno nenaučí. Pro zájemce zde je více informací o kompilování [odkaz]. Časy běhu jsem získal pomocí Linuxového programu time [man] takto:
c:/cygwin/bin/time python konvertor.py rp01.zrdnebo
c:/cygwin/bin/time python konvertor.pyc rp01.zrdnebo
c:/cygwin/bin/time ./bfc.exe rp01.zrd _
kde za _ jsem postupně dával písmenka (
Pro nás ostatní a díky Pavlickovi existuje tato snadnější cesta, neb i on doznal, že je to těžké (formát pro vyřešená symetrická rozdání jsem pro účely tohoto článku vzdal).
Nejjednodušší vlastně byla jen kontrola integrity binárně načteného souboru pomocí součtu hexadecimálních čísel úseků, v našem případě tedy bajtů seřazených od konce, kdy úseky sčítanců tvořilo 32 bitů (čtyři bajty). Ty bajty musely být přeházené, protože jedno rozdání tvoří 23 bajtů a toto číslo není dělitelné čtyřmi, takže na pořadí bajtů záleží neb se ty čtveřice lomí.
Co víc si člověk může přát? Na mé návrhy (tyto dva hádankářské binární formáty z BIN na ZRD+ZSD v prvním kole), spíš stavy zoufání, rozšířil Pavlicek svůj konvertor, v druhém kole i o formát pro program Deal se zkratkou
Když tedy vyzkoušíme na první části Pavlickova archivu:
python konvertor.py rp01.zrd
bfc.exe rp01.zrd i
diff out.ddl 2overen.txt
Zjistíme, že jsou naše výstupy identické na úrovni bitů. Z vědeckého pohledu uvažování bychom měli též ověřit, jestli Pavlicek nepoužívá stejnou DD knihovnu jako program Deal [odkaz], tedy DDS knihovnu Bo Haglunda (je to C++ zdrojový kód a měl dříve přes 100 tisíc znaků; odkaz, resp. knihovny jsou zde, v Linuxovém repozitáři pod klíčovým slovem DDS jsem tyto zdrojové kódy neobjevil). Pokud ano, pak bychom srovnávali výsledky vzniklé ze stejného zdroje (ať už by tam byly chyby či nikoliv) a tento článeček můžeme hodit do koše. Pryč s ním! Kdyby tam totiž byla chyba, tak se objeví na obou výstupech a my bychom je prohlásili oba za správné, neb by byly výstupy identické, ale my bychom je chybně považovali za nezávislé. Tref by člověka trefil!
Zde je ukázka běžícího DDS v Linuxu:
dds deals.gib -deal=1
nebo
dds deals.gib -timeall
Od jedné až po rozdání 4. Soubor je uložen v /usr/share/doc/dds/examples/. Případně po rozpakování test.gib.gz v tom samém adresáři:
dds test.gib -timeall
nebo úplnou DD tabulku pro jedno rozdání:
dds test.gib -name=giblib1 -tricks
dds test.gib -deal=16 -tricks
nebo pro víc rozdání:
dds test.gib -giblib=1-25-all
DD řešení je v posledním řádku u jednotlivých rozdání.

Poněvadž mám roky v hlavě tajný nápad na měření obtížnosti bridžového rozdání (jistá vize to je, reálné to asi bohužel není, ani Bo Haglund to růžově nevidí), tak k tomu byly potřeba zdrojové kódy, aby se dalo dostat do celého rozhodovacího stromu a mezivýpočtů. Ty byly právě u Aleaxe [odkaz], po rozbalení dds10.zip [odkaz] se to z C++ zdrojových kódů sice pohlo:
sudo python setup.py install
python trydds.py
Ale stejně jsem s tím nepohnul... To chce programátora. Poslední verze zdrojových kódů [odkaz] z března 2013 má už přes 200 tisíc znaků, v tom se nedá vrtat, ve stavu zoufání píši autorovi, jestli by mi nepomohl, nezpřístupnil mezivýpočty či nějakou formu ladění (to má ve zdrojovém kódu připravené, ale je to tam vypnuté). Tak poctivě jsem rekurzi či nějaký alternativní postup nestudoval. Bohužel po letech docházím k závěru, že se dá měřit časová náročnost díky rozhodovacímu stromu, ale na měření obtížnosti z karetního pohledu to nebude.
Nu, užijte si 10.485.760 zanalyzovaných rozdání! Ještě píši Pavlickovi, jestli by nepřidal do svého BFC konvertoru originální Ginsbergův formát s příponou ASC (navrhl jsem zkratku písmene
Aktualizováno 11. 6. 2013: Verze BFC 4.4 je na světě! [web, poznámky, program]
Hi Pavel,
I finally got around to adding the two Ginsberg DD formats (ASC,BIN). The problem was deciding on file extensions, as I had used .ASC for BFC's template files, and I use .BIN for many things (as does the world). I decided to rename BFC'S template files to .BFC (that makes sense) but .BIN was too valuable for Ginsberg's stupid format (26 bytes when only 23 are necessary)... so I christened his binary files as .GDD = Ginsberg double-dummy or Type G. The ASCII format is .ASC or Type A.
-Richard
R.I.P. pro ty, kteří umřeli při četbě tohoto příspěvku. Autor příspěvku se jen za přispění Daidalose, samotného tvůrce, dostal z tohoto labyrintu...
P.S. Nyní mohu klidně umřít, s pokladem v rukách...
Velký konvertor alias
konvertor.py [
konvertor.pyc [
Zde je celý adresář všech zmíněných souborů
konvertor.rar [
Děkuji Tiboru Menyhértovi za připomínky, dle možností jsem je zapracoval. Člověk se na tom bridžovém ostrově necítí alespoň tak sám.